Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋くんは自分の年齢を忘れてしまいました。
ひとまず 3 人の友達を集めることに成功したので、その 3 人が予想する高橋くんの年齢の中央値を、高橋くんの年齢として代用することにしました。
高橋くんに代わって 3 つの整数 a, b, c から中央値を求めるプログラムを書いてください。
3 つの整数の中央値とは、それらを小さい順に並べて中央に位置する整数のことです。
入力
入力は以下の形式で標準入力から与えられる。
a b c
- 3 つの整数 a, b, c (1 ≦ a, b, c ≦ 100) が空白区切りで与えられる。
出力
a, b, c の中央値を標準出力に出力せよ。
末尾の改行を忘れないこと。
入力例1
2 3 4
出力例1
3
2, 3, 4 の中央値は 3 です。
入力例2
5 100 5
出力例2
5
5, 100, 5 の中央値は 5 です。
入力例3
3 3 3
出力例3
3
入力例4
3 3 4
出力例4
3
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋くんはある文字列 s を持っています。文字列を短く表現することに興味のある高橋くんは、以下の圧縮方法を試してみることにしました。
- 文字列 s を同じ文字が連続する文字列に分割します。(分割)
- 分割された各文字列を、文字と、その文字が連続する長さをつなげた新たな文字列に変換します。(変換)
- 最後に、変換した各文字列を前から順に結合します。(結合)
aabbbaad という文字列に上記の圧縮方法を適用すると
aabbbaadをaabbbaadに分割aabbbaadを、それぞれa2b3a2d1に変換a2b3a2d1をa2b3a2d1と結合
以上より、a2b3a2d1 を得ることができます。
あなたには文字列 s が与えられるので、上記の方法で圧縮された文字列を求めるプログラムを、高橋くんの代わりに書いてください。
入力
入力は以下の形式で標準入力から与えられる。
s
- 圧縮する文字列 s (1 ≦ |s| ≦ 1,000) が与えられる( |s| は文字列 s の長さを表す)。
- s は英小文字から成る文字列であることが保証される。
出力
s から作られた圧縮された文字列を標準出力に出力せよ。
末尾の改行を忘れないこと。
入力例1
aabbbaad
出力例1
a2b3a2d1
問題文中の例です。
入力例2
aabbbbbbbbbbbbxyza
出力例2
a2b12x1y1z1a1
長さは10進表記です。
入力例3
edcba
出力例3
e1d1c1b1a1
圧縮された結果、元の文字列より長くなることもあります。
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋くんは魔法の箱を持っています。
この箱に整数を入れるとそれに対応した整数が出てきます。
出てくる整数は入れた整数だけによって決まり、同じ整数を入れると毎回同じ結果が得られます。
高橋くんは任意の整数 x について、x を入れた時と 2x を入れた時に出てくる整数が同じであることに気づきました。
高橋くんが入れた整数が N 個与えられるので、最大で何種類の整数が出てくるか答えてください。
入力
入力は以下の形式で標準入力から与えられる。
N a_1 a_2 .. a_N
- 1 行目には、高橋くんが箱に入れる整数の個数 N ( 1 ≦ N ≦ 10^5) が与えられる。
- 2 行目には、高橋くんが箱に入れる N 個の整数が空白を区切りとして与えられる。
- 1 ≦ a_i ≦ 10^9 ( 1 ≦ i ≦ N) であることが保証される。
- i ≠ j のとき、a_i ≠ a_j であることが保証される。
出力
最大で何種類の整数が出てくるかを標準出力に出力せよ。
末尾の改行を忘れないこと。
部分点
この問題には部分点が設定されている。
- 20 点分のテストケースにおいて、1 ≦ N ≦ 3,000 を満たす。
- 別の 30 点分のテストケースにおいて、1 ≦ a_i ≦ 5*10^5 ( 1 ≦ i ≦ N) を満たす。
入力例1
3 1 2 3
出力例1
2
2 を入れた時に出てくる整数は、1 を入れた時に出てくる整数と等しいので、最大で 2 種類の整数が出てきます。
入力例2
4 2 4 8 16
出力例2
1
すべて同じ整数が出てきます。
入力例3
4 2 3 5 7
出力例2
4
出てくる整数が全て違う可能性があります。
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋くんは木の直径を求めるのに夢中です。 木とは、頂点とそれを結ぶ辺からなる構造「グラフ」の 1 種で、頂点の数を N 個とすると、辺は N-1 本あり、どの頂点も他の全ての頂点に辺で間接・直接的につながっています。
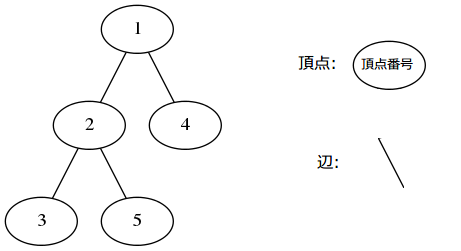
この問題では、辺には整数の重みがついています。2頂点の間の距離を、その2つの頂点をつなぐ辺の重みの和と定義します。
木の直径とは、最も離れた2つの頂点の間の距離です。
以下のような木を考えてみましょう。辺の側に書かれた数が、その辺の重みです。
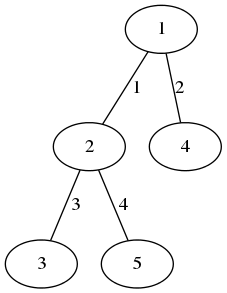
この場合、頂点 1 と 2 の距離は 1、頂点 2 と 4 の間の距離は 1+2=3 となります。頂点 3 と 5 の間の距離は 3+4=7、頂点 4 と 5 の間の距離も 2+1+4=7 で、この距離がこの木の頂点の間では最大なので、木の直径は 7 となります。
高橋くんは、頂点の数と 2 頂点間の距離の情報から、木の直径を求めることに興味が出てきました。 この問題では、あなたは木の頂点の数 N を最初に与えられ、2 頂点の間の距離を尋ねる質問を何回か行い、木の直径を求めます。
ただし、2 頂点間の距離を聞く回数には制限があります。
制限された質問の回数以内で木の直径を求めるプログラムを書いてください。
入出力
まず,木の頂点の数 N が標準入力に与えられる。
N
続いて,あなたのプログラムは何回か応答プログラムに質問をする.質問のフォーマットは以下のとおりである。
? a b
この質問で,a,b 間の距離が標準入力に1行で渡される。1 ≦ a, b ≦ N かつ a≠b を満たしていなければならない。
何回か質問を行った後、あなたは木の直径を当てる。木の直径を diameter とおくと、
! diameter
というフォーマットで出力する。木の直径を出力した後、あなたのプログラムは直ちに終了しなければならない。終了しなかった場合のジャッジ結果は不定である。
また、これら以外のフォーマットで出力した場合のジャッジ結果も不定である。
この問題ではテストケースごとに質問回数の上限値が設定されており、プログラムの行った質問の回数がその上限値を上回ると誤答と判定される。
正答かどうかは木の直径の出力で判断される。木の直径を特定し得ない質問しかしていない場合でも、直径が正しければ正答となる。
頂点 1 と頂点 2 の間の距離を質問し、dist という変数で結果を受け取る例をいくつかの言語について示す。
ただし、ここに書かれている方法以外で入出力を行っても良い。
出力した後に、出力をflushしなければならないことに注意せよ。flushしなかった場合、TLEとなることがある。
C
printf("? %d %d\n", 1, 2);
fflush(stdout);
scanf("%d", &dist);
C++
cout << "? " << 1 << " " << 2 << endl; cin >> dist;
Java
System.out.printf("? %d %d\n", 1, 2);
Scanner scanner = new Scanner(System.in);
dist = scanner.nextInt();
C#
Console.WriteLine("? {0} {1}", 1, 2);
dist = int.Parse(Console.ReadLine());
D
writeln("? ", 1, " ", 2);
stdout.flush();
dist = readln.chomp.to!int;
PHP
echo "? ", 1, " ", 2, PHP_EOL; $dist = trim(fgets(STDIN));
Python
print "? {0} {1}".format(1, 2)
sys.stdout.flush()
dist = int(raw_input())
Perl
$|=1; print "? ", 1, " ", 2, "\n"; $dist = <>;
Ruby
print "? ", 1, " ", 2, "\n" STDOUT.flush dist = gets.to_i
制約
- 2 ≦ N ≦ 50
- 1 ≦ (それぞれの辺の重み) ≦ 10^6
部分点
この問題には部分点が設定されている。
- 20 点分のテストケースにおいて、質問回数の上限値は 1300 回である。
- 別の 80 点分のテストケースにおいて、質問回数の上限値は 100 回である。
入出力例
木が以下のような形状のとき、
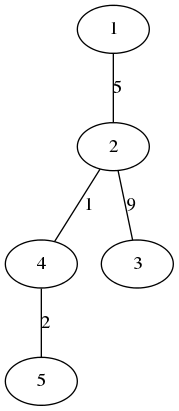
以下のような入出力が考えられる。
| プログラムへの入力 | プログラムの出力 |
|---|---|
| 5 | |
| ? 1 2 | |
| 5 | |
| ? 2 4 | |
| 1 | |
| ? 4 5 | |
| 2 | |
| ? 2 3 | |
| 9 | |
| ? 1 5 | |
| 8 | |
| ! 14 |
これは入出力の一つの例であり、意味のある質問をしているとは限らない。