 /
/ 
Time Limit: 3 sec / Memory Limit: 1024 MiB
問題文
縦 N 個、横 N 個の正方形上にならんだ N × N 個のパネルがあります。あなたは、このパネルを使ってゲームを行います。
このゲームは、出来るだけ全てのパネルの色を 1 色に揃える事が目的です。最初、各パネルは、色 1 から 色 K の K 色で塗られています。
好きな色を念じながら 1 つのパネルをタッチすることで、そのパネルを好きな色に変えることができます。タッチしたパネルの色を i、変えたい色を j とします。 この時、タッチしたパネルから、上下左右に隣接する色 i のパネルだけを辿って到達できる全てのパネルは、色 j に変化します。
このゲームの最終得点は、以下のような計算式で求められます。
- 最も多いパネルの色を i とすると、色 i のパネルが 1 枚存在するごとに、100 点を得る。
- パネルを 1 回タッチするごとに 1 点を失う。
- ただし、パネルを合計 10000 回より多くタッチすると、システムが壊れてしまうため、0 点となる。
パネルの初期状態が与えられます。タッチの仕方を出力し、出来るだけ多くの得点を獲得してください。
なお、この問題は、入力が全て公開されており、また、全ての入力に独立な通し番号idがついています。これを利用して問題を解いても構いません。
また、C++によるジャッジ上で実際に動いている入出力チェッカーも公開しています。こちらを利用しても構いません。
制約
- 1 ≦ id ≦ 50
- N = 100
- K = 9
- S_i は N 文字の文字列であり、 j 番目の文字 S_{i,j} は、
1~Kの K 種類である。これは、上から i 番目、左から j 番目(以下(i,j)と表す)のパネルがS_{i,j} 色であることを表す。 - S に使われる文字は、
1~Kまで、均等な確率で独立にランダムで選ばれる。 - 入力はこのリンクから得られるzipファイルと同一のものが与えられる。
入力
id N K S_1 S_2 : S_N
出力
以下のフォーマットで出力せよ。ただし、Q はパネルをタッチする回数を表し、Y_i, X_i, C_i はそれぞれ、i 番目にタッチするパネルが、上から Y_i 番目、左から X_i 番目(以下、(Y_i, X_i) と表す)であり、変える色が C_i であることを表す。
Q Y_1 X_1 C_1 Y_2 X_2 C_2 : Y_Q X_Q C_Q
50 個のテストケースに対する点数の和が、あなたの提出の得点となる。
入力例 1
0 6 9 515795 153859 833597 333419 333121 533917
出力例 1
2 5 5 1 5 2 1
この入力は、説明のため、実際には存在しない小さい入力を使用しております。
パネルは、初期状態では以下のようになっています。
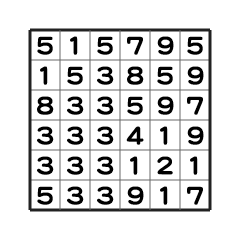
ここから出力の通りに 2 回タッチします。
最初は、(5,5) のパネルを色 1 に変えます。この時、隣接するパネルの中で、元のパネルの色である、色 2 のものは存在しないため、このパネルのみの色が変わります。
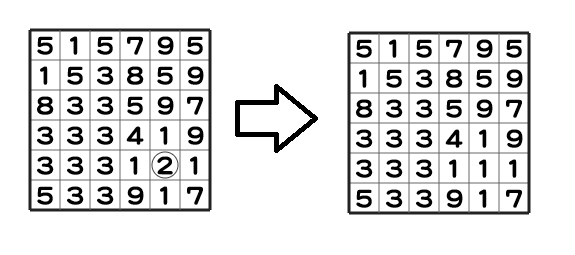
次に、(5,2) のパネルの色を 1 に変えます。この時、上下左右に隣接した色 3 のパネルを辿って到達できる全てのパネルは、色 1 に変化するため、以下のようにパネルが変化します。
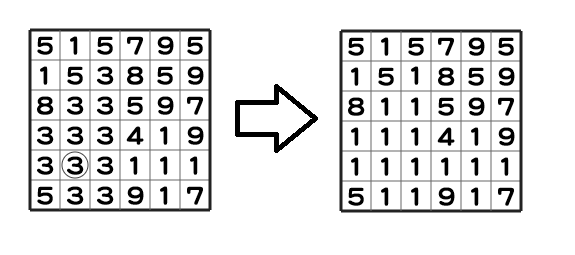
全てのパネルを操作した後、最も多い色のパネルは色 1 であり、この枚数は 18 枚です。
よって、18 × 100 - 2 = 1798 点が、この解の答えになります。