 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 500 点
問題文
高橋君は 1 辺の長さが N の 3 枚の鏡を正三角形状に組み合わせました。 三角形の頂点をそれぞれ a, b, c とします。
高橋君は、辺 ab 上の頂点 a から X の点から、辺 bc と平行に不思議な光を発射しました。 不思議な光は、普通の光と同じように真っすぐ進み、鏡に当たると反射するのですが、不思議な光がすでに通った点に当たったときにも反射をします。 例えば、N = 5, X = 2 のとき、不思議な光の軌跡は図の黄色い矢印のようになります。
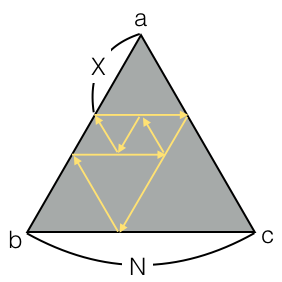
このように不思議な光を発射した時、不思議な光は必ず発射した点に戻ってくることが証明できます。 このとき、光の軌跡の長さが全体でいくらになるかを求めて下さい。
制約
- 2≦N≦10^{12}
- 1≦X≦N-1
- N と X はいずれも整数である。
部分点
- N≦1000 を満たすデータセットに正解した場合は、300 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 200 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N X
出力
光の軌跡全体の長さを出力せよ。
入力例 1
5 2
出力例 1
12
問題文中の図のとおりです。 光の軌跡の長さは全体で 2+3+2+2+1+1+1 = 12 となります。
Score : 500 points
Problem Statement
Snuke is conducting an optical experiment using mirrors and his new invention, the rifle of Mysterious Light.
Three mirrors of length N are set so that they form an equilateral triangle. Let the vertices of the triangle be a, b and c.
Inside the triangle, the rifle is placed at the point p on segment ab such that ap = X. (The size of the rifle is negligible.) Now, the rifle is about to fire a ray of Mysterious Light in the direction of bc.
The ray of Mysterious Light will travel in a straight line, and will be reflected by mirrors, in the same ways as "ordinary" light. There is one major difference, though: it will be also reflected by its own trajectory as if it is a mirror! When the ray comes back to the rifle, the ray will be absorbed.
The following image shows the ray's trajectory where N = 5 and X = 2.

It can be shown that the ray eventually comes back to the rifle and is absorbed, regardless of the values of N and X. Find the total length of the ray's trajectory.
Constraints
- 2≦N≦10^{12}
- 1≦X≦N-1
- N and X are integers.
Partial Points
- 300 points will be awarded for passing the test set satisfying N≦1000.
- Another 200 points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
N X
Output
Print the total length of the ray's trajectory.
Sample Input 1
5 2
Sample Output 1
12
Refer to the image in the Problem Statement section. The total length of the trajectory is 2+3+2+2+1+1+1 = 12.