2べきの整数 \(B\) を用いて \(N\leq B^2\) かつ \(N\) が \(B\) の倍数であるとします。（一般の \(N\) から \(O(\sqrt{P}\log P)\) 時間で帰着します。）

寄与をグリッドで表します。左から右に向かって各列に \(1,2,\ldots , N\) を割り当てます。各列についてその値をかける個数だけマスを配置します。 \(k\) は \(N+1-k\) 回掛かるので、階段状に表せます。

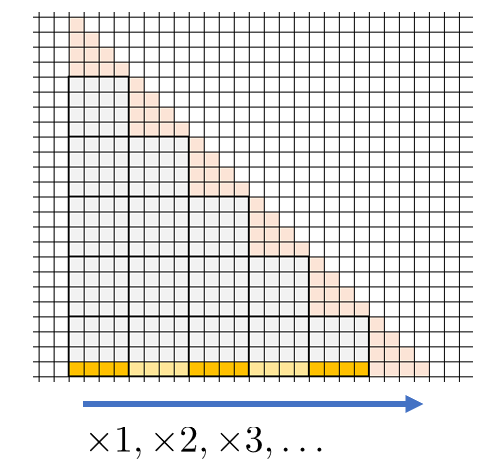
よくある階乗前計算で得られるものは、例えば \(f(x)=\prod _ {k=1}^{B}(Bx+k)\) としたときの \(f(0),f(1),\ldots ,f(B-1)\) です。これは上図では一番下の黄色の行に対応します。これを使えば、グリッド全体のうち赤色の小さな階段以外の部分を計算できます。

赤色の階段部分は、下図のように、同じ形どうしの対応する部分を掛けた値（ \(B\) 個、下図の下半分の行ごとに総積をとる）があれば、赤色部分全体の寄与を得られます。

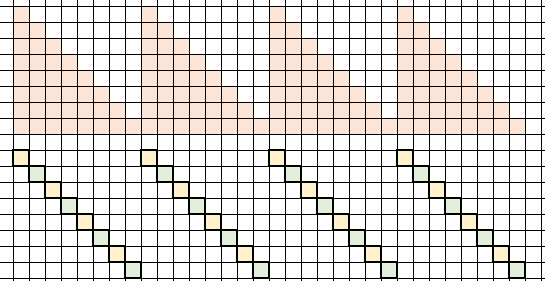
式にすると、 \(g(x)=\prod _ {k=0}^{N/B-1}(x+Bk)\) としたときの \(g(0),g(1),\ldots ,g(B-1)\) です。これは階乗前計算と同様の方法で、すなわち、多項式を \(x=0,1,\ldots ,\) で評価した値を管理しながらの taylor shift を用いれば \(O(\sqrt{P}\log P)\) 時間で求まります。